
|
Die Ausgangsfrage für dieses Experiment war:
"Kann man diesen 7N-Stator als 3-Phasenwchselstrommotor mit 4 Magnetpolpaaren sauber zum Laufen bringen?"
Die Antwort heisst(wie meistens):
|
|
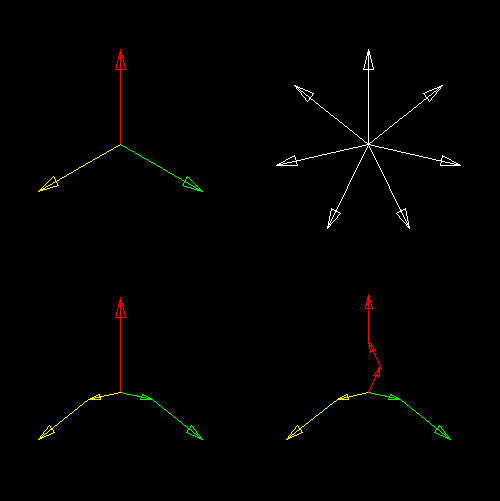
Bei einem 'richtig' symmetrischen Motor sind im Zeigerdiagramm, das Spannungen und Phasenbeziehungen darstellen kann, die Phasenspannungen eines Motors sauber mit 120° zueinander angeordnet (oben links). Ein 7N-Stator bietet 7 verschiedene Phasen (oben rechts), wobei durch umgekehrten Wicklungssinn natürlich auch die jeweils um 180° gedrehten Spannungen zur Verfügung stehen. Die gewünschten Spannungen und Phasen kann man jetzt durch Vektoraddition der zur Verfügung stehenden Spannungen zusammenstellen(unten links). Letztlich würde aber auch die 'obere' Phase durch Teile anderer Spannungen zusammengestellt, teils, um den exakten Spannungsverlauf zu formen, teils um nicht auf einem Zahn sehr viele Windungen wickeln zu müssen, und auf anderen gar keine (unten rechts). Das 'verteilen' entspricht beinahe dem Wickeln einer verteilten LRK-Wicklung im Vergleich zu einer 'echten' LRK. |
|
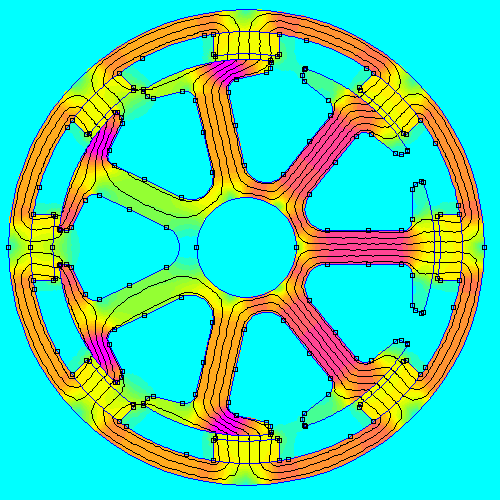
Mit FEMM wurden 606 Simulationen für 5 verschiedene 7N8P und 484 Simus für 4 7N10P Varianten theoretisch getestet. Die Drehteile für einen 7N 10P liegen nämlich auch schon da. |
|
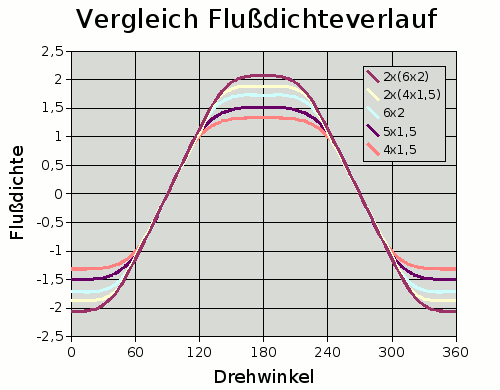
Bei jeder FEMM-Rechnung wurden die Flußdichten in den Zähnen bestimmt. dann wurde der Rotor ein kleines stück gedreht, und die nächste Sim gerechnet. So entstanden 9 Kurven der Flußdichte in den Zähnen. (Hier nur die 8P-Varianten) |
|
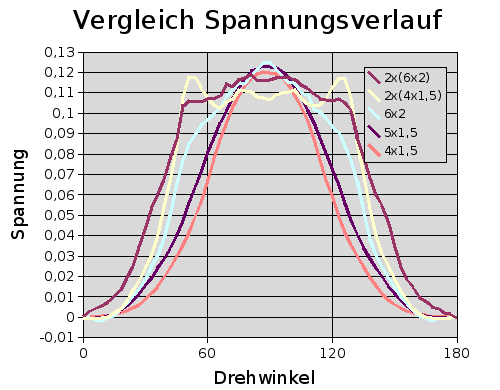
Im nächsten Schritt wurden die Spannungen bestimmt, die in einer Wicklung auf einem Zahn induziert wird. Die Spannung ist proportional zur änderung des Flusses, und kann so aus der Differenz zweier benachbarter Werte bestimmt werden. |
|
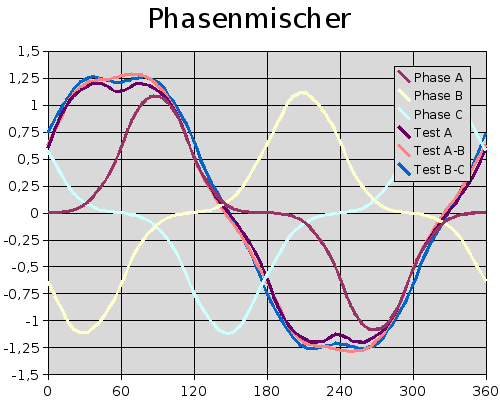
Dann wurden diese Spannungen genau so zusammengemischt, wie es vorher anhand der Zeigerdiagramme bestimmt wurde. Außerdem wurde dabei auch gleich noch ausgerechnet, wie die Spannungen an den Klemmen aussehen werden. Die Rechnung im Zeigerdiagramm berücksichtigt immer nur die Grundwelle. Da hier auch Oberwellen berücksichtigt werden, kann ein erster Optimierungsschritt erfolgen. Auf dem Bild sieht man die einzelnen Spannungen, zwischen Stern und Motorklemme. Dazu wurde noch eine Kurve 'Test A' errechnet, die eine reine bewertung des Spannungsverlaufes der Phase 'A' zuläßt. Test AB beschreibt dann die tatsächlich meßbare Spannung zwischen den Motorklemmen A und B, Test BC entsprechend. |
|
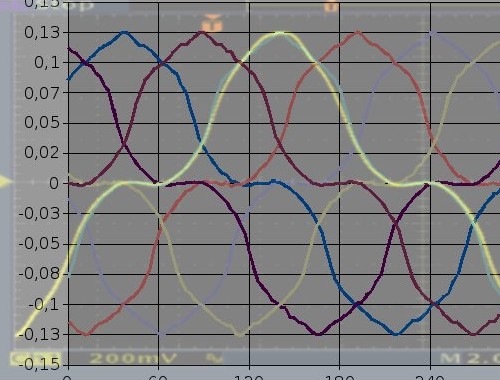
Nach viel trockener Theorie erfolgte dann die Messung der Spannung, die an einem Zahn induziert wird. Die messung wurde mit der Wicklung aus dem obersten Bild gemacht. Vor allem sollte das zeigen, ob die FEMM-Rechnung halbwegs vernünftige Ergebnisse liefert. Dafür, daß keine Materialdaten zur Verfügung standen, und auch die Magnetstärke nicht (mehr) bekannt war, entspricht der gemessene Kunververlauf (gelb über das andere Bild gelegt) recht gut den errechneten Werten. |
|
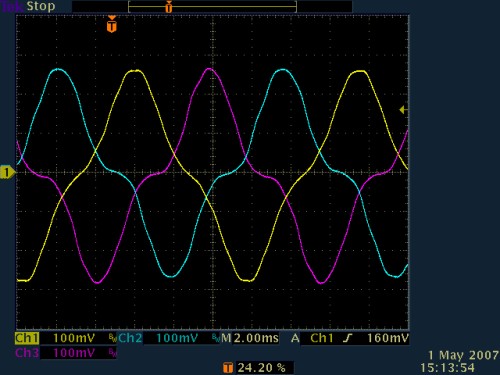
Nach erfolgreichem Test einer einzelnen Spannnung wurde dann die erste 3-Phasen-Meßwicklung gewickelt. Hier wurden 2 Varianten getestet, einmal mit konzentrierter 'A'-Phase, einmal verteilt. Dabei wurde auch festgestellt, daß gegenüber der (schon genaueren) Rechnung die Windungsanzahl noch etwas korrigiert werden mußte. Rechnung und Realität weichen eben doch etwas voneinander ab. Auf dem Bild sieht man die Phasenspannungen der 3 Wicklungen. |
|
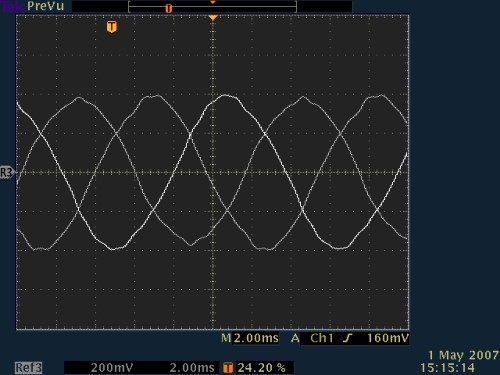
Recht interessant an den Phasenspannungen ist, daß es nicht unbedingt notwendig ist, schön sinusförmige Phasenspannungen zu haben. Der Motor wird nur an den Motorklemmen angeschlossen, also ist auch nur wichtig, schön geformte Klemmenspannungen zu haben. Die Klemmenspannung ist (bei Stern) immer die Differenz von 2 Phasenspannungen. Auf dem Bild sieht man die Klemmenspannungen, wie sie hier das Oszi aus den Phasenspannungen ausgerechnet hat. Damit waren die Berechnungen und Tests abgeschlossen. |

|
Der bewickelte Stator.
Das Schema lautet: AaABbcC die Windungszahlverhältnisse zur Korrektur der Asymmetrien dazu: 3 5 3 7 3 3 7. Die A- Phase wurde also im Ergebnis der Optimierung um einen Tick "verstärkt".
Summen der Windungszahlen der Phasen im Vergleich:
|

|
Bei ersten Test stellte sich heraus, daß die ursprünglich geplante Glocke doch etwas zu weich war, also wurde noch ein schöner, natürlich 7-armiger Glockenboden hergestellt. |

|
7N8P... |

|
...und er dreht sich doch ;-) ohne dem Steller besondere Schwierigkeiten zu bereiten. hinsichtlich seiner Leistungsfähigkeit ist er noch nicht vermessen, aber das war ja auch nicht die Fragestellung beim Experiment. |